Backpropagation is often introduced in the context of deep neural networks, which can make it appear complex and intimidating. However, at its core, backpropagation is simply an efficient application of calculus specifically the chain rule to optimize model parameters.
Consider a dataset with one input feature x and one output y.
The linear regression model is defined as:
$$ \hat{y} = f(x) = wx + b $$To measure how good or bad the model’s prediction is, we use a loss function.For simplicity, we choose Mean Squared Error (MSE) for a single data point:
Loss function:
$$ L = (y - \hat{y})^2 $$Substituting the model equation:
$$ L = (y - (wx + b))^2 $$The objective of training is to minimize this loss by adjusting w and b.
Backpropagation answers one question:How should the parameters w and b change to reduce the loss?
To answer this, we compute the gradients of the loss with respect to the parameters:
$$ \frac{\partial L}{\partial w}, \quad \frac{\partial L}{\partial b} $$These gradients tell us: the direction of change the rate at which the loss changes
The loss depends on 𝑤 and 𝑏 indirectly through the prediction 𝑦.This is where the chain rule is used.
Step 1: Gradient of Loss w.r.t Prediction
$$ \frac{\partial L}{\partial \hat{y}} = -2 (y - \hat{y}) $$This term represents how sensitive the loss is to the prediction error.
Step 2: Gradient of Prediction w.r.t Parameters
from:
$$ \hat{y} = wx + b $$we get
$$ \frac{\partial \hat{y}}{\partial w} = x $$ $$ \frac{\partial \hat{y}}{\partial b} = 1 $$Step 3: Final Gradients (Backpropagation)
using the chain rule
Gradient w.r.t Weight:
$$ \frac{\partial L}{\partial w} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial w} = -2 (y - \hat{y}) x $$Gradient w.r.t Bias
$$ \frac{\partial L}{\partial b} = \frac{\partial L}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial b} = -2 (y - \hat{y}) $$this is the part called as propagation
one gradients are computed, parameters are updated using gradient descent.
$$ w := w - \alpha \frac{\partial L}{\partial w} $$ $$ b := b - \alpha \frac{\partial L}{\partial b} $$where α is the learning rate.
This step moves the parameters in the direction that reduces the loss.
Code
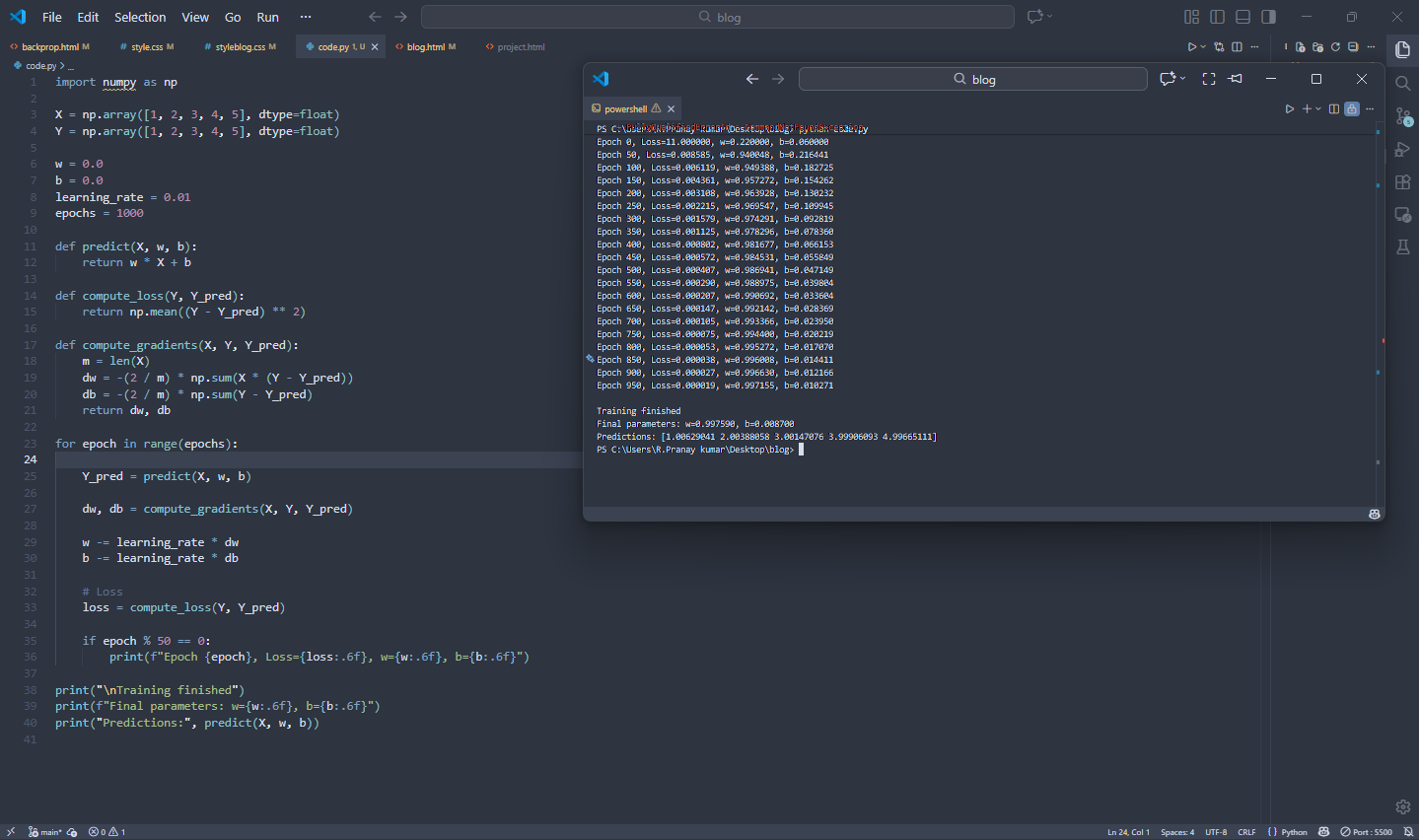
import numpy as np
# Data
X = np.array([1, 2, 3, 4, 5], dtype=float)
Y = np.array([1, 2, 3, 4, 5], dtype=float)
# Parameters
w = 0.0
b = 0.0
learning_rate = 0.01
epochs = 1000
# Forward pass
def predict(X, w, b):
return w * X + b
# Loss
def compute_loss(Y, Y_pred):
return np.mean((Y - Y_pred) ** 2)
# Backpropagation (Batch Gradients)
def compute_gradients(X, Y, Y_pred):
m = len(X)
dw = -(2 / m) * np.sum(X * (Y - Y_pred))
db = -(2 / m) * np.sum(Y - Y_pred)
return dw, db
# Training loop
for epoch in range(epochs):
Y_pred = predict(X, w, b)
dw, db = compute_gradients(X, Y, Y_pred)
w -= learning_rate * dw
b -= learning_rate * db
loss = compute_loss(Y, Y_pred)
if epoch % 50 == 0:
print(f"Epoch {epoch}, Loss={loss:.6f}, w={w:.6f}, b={b:.6f}")
print("\nTraining finished")
print(f"Final parameters: w={w:.6f}, b={b:.6f}")
print("Predictions:", predict(X, w, b))
Backpropagation is not exclusive to neural networks it exists even in the simplest linear regression model. In this single-function case, backpropagation reduces to applying the chain rule to compute gradients efficiently.